- Ruhr-Universität Bochum
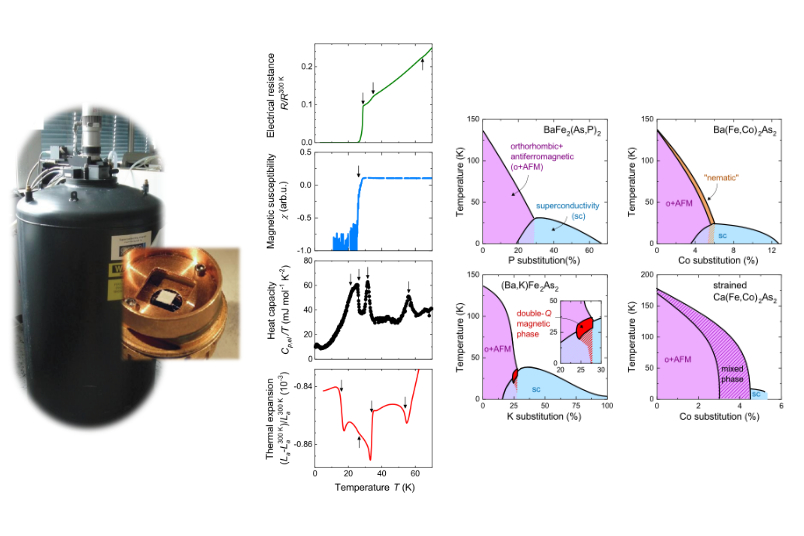
Basic property measurements for intricate physical phase diagrams
Many quantum materials exhibit intricate physical phase diagrams, where a slight change of an external parameter might make the difference between the material being a magnetic insulator or a high-temperature superconductor. This external parameter (so-called “tuning” parameter) can be the material composition, external pressure, or a magnetic field, to name the most common examples. We have investigated the intricate phase diagrams realized by tuning materials of the family of the iron-based superconductors using basic physical property measurements over the past years.
The electrical resistance is a basic property which, when measured at sufficiently high resolution, can signal almost any phase transition. In particular, its vanishing is a hallmark of superconductivity. In addition, magnetic susceptibility measurements serve to identify superconductivity, but also ferro- or antiferromagnetic phases. Measurements of the specific heat capacity are a prime method to assess a phase transition, since they help to quantify the entropy changes involved. The high-resolution measurement of the thermal expansion is also very useful to find and assess phase transitions. Overall, at least minor anomalies (such as peaks steps or kinks) will occur at a phase transition in all physical properties. When the phase lines have been found with the basic property measurements, more advanced techniques, such as diffraction or imaging, are used to identify the still unknown phases.
A widely-used, robust, reliable and high-precision machine for such measurements is a Physical Property Measurement System (aka “PPMS”), which has been pioneered by Quantum Design, Inc. It allows to control and rapidly modify the temperature and magnetic field environment of the sample, while different options enable the physical measurements, including electrical transport, magnetization, or heat capacity.
We have used physical property measurements to outline the composition-temperature phase diagrams of many iron-based superconductors [1]. In general, these phase diagrams look similar with superconductivity occurring in a dome-like area that peaks when an antiferromagnetic and orthorhombic phase is suppressed. However, variations of this theme hold clues for understanding of how these phases come to be. For example, whereas in some materials a tetragonal-to-orthorhombic structural transition coincides with an antiferromagnetic one, the two transitions split in others and the structural transition precedes the magnetic transition. This sparked the extremely active field of “nematicity” in these material systems, which we discussed [2]. Moreover, our investigations revealed a small pocket of a new exotic “double-Q” magnetic phase in one iron-based system and discovered superconductivity acts to suppress it again [3]. With up to four subtle phase transitions between 20 - 60 K, the combination of high-resolution thermal expansion, heat capacity and susceptibility measurement was indispensable for identifying the phase lines. Finally, we could identify a mixed-phase region in an extremely strained system [4].
All in all, basic physical properties allow to characterize in detail the average state of a material. Thus, they leverage their full power when highly homogeneous samples, most often single crystals, are under investigation. They are the basis, on which more advanced studies of electronic band dispersions, magnetic textures and propagation vectors, or quasiparticle excitation spectra – to name just a few – build.
[1] Anna Böhmer und Andreas Kreyssig, Unkonventionelle Hochtemperatur-Supraleitung: Eisenbasierte Vielfalt, Physik in unserer Zeit 2/2017 (2017). DOI: 10.1002/piuz.201701462
[2] Anna E. Böhmer, Jiun-Haw Chu, Samuel Lederer and Ming Yi, Nematicity and nematic fluctuations in iron-based superconductors, Nature Physics 18, 1412 (2022)
[3] A. E. Böhmer, F. Hardy, L. Wang, T. Wolf, P. Schweiss, C. Meingast, Superconductivity-induced reentrance of orthorhombic distortion in Ba1-xKxFe2As2, Nature Communications 6, 7911 (2015)
[4] A. E. Böhmer, A. Sapkota, A. Kreyssig, S. L. Bud'ko, G. Drachuck, S. M. Saunders, A. I. Goldman, and P. C. Canfield, Effect of biaxial strain on the phase transitions of Ca(Fe1-xCox)2As2, Phys. Rev. Lett. 118, 107002 (2017)
